Le théorème des valeurs intermédiaires est d’une grande importance en analyse. Il permet notamment de montrer qu’une équation possède des solutions même s’il est impossible de les expliciter. Un des formes du théorème dit que « si une fonction f est définie et continue sur [a;b] alors pour tout réel c appartenant à [f(a) ;f(b)], l’équation f(x) = c possède au moins une solution ».  Le théorème tire son nom du fait qu’il montre que toutes les valeurs intermédiaires c dans [f(a);f(b)] sont « atteintes » en balayant [a;b].

Le théorème de Bolzano en propose une forme simplifiée. Il nous dit que « si f(a) et f(b) sont de signe opposé, autrement dit si f(a)f(b) < 0, alors l’équation f(x) = 0 possède au moins une solution » (c, qui vaut 0 dans ce cas particulier, appartient bien à [f(a) ;f(b)]).

La force du théorème des valeurs intermédiaires et de celui de Bolzano réside dans le fait que les conditions qu’ils imposent sont applicables à toutes les fonctions usuelles, qui sont continues sur au moins des sous-intervalles de leur ensemble de définition.

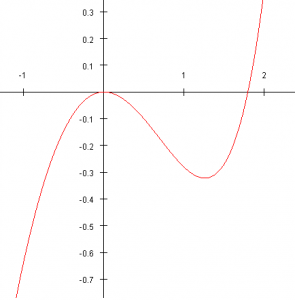
Ces deux théorèmes s’illustrent aisément grâce aux représentations graphiques. Considérons par exemple la fonction f : x↦e^x-x²-x-1, représentée ci-contre. Il est aisé de montrer qu’elle est définie et continue sur [-1 ;2] et que f(-1)f(2) < 0. Par conséquent, l’équation e^x-x²-x-1 = 0 admettra au moins une solution sur [-1 ;2]. En pratique, comme le laisse supposer la courbe, elle en admettra deux : 0 (solution évidente) et une seconde qu’il n’est pas possible d’expliciter.

Afin de démontrer l’existence d’une solution unique sur un intervalle donné, il faut rajouter une condition supplémentaire au théorème des valeurs intermédiaires, connue sous le nom de corollaire : « si la fonction est en plus strictement monotone sur [a;b] (c’est-à-dire strictement croissante ou strictement décroissante) alors l’équation f(x) = c, ou f(x) = 0, admet une unique solution ». On peut par exemple appliquer ce corollaire à notre fonction f: x↦e^x-x²-x-1 sur l’intervalle [3/2;2].

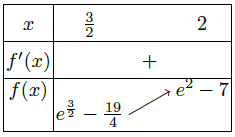Le tableau de variations ci-contre nous montre en effet que la fonction f est strictement croissante sur [3/2;2] et la calculatrice donne facilement f(3/2) < 0 et f(2) > 0. Par conséquent, l’équation f(x) = 0 admet une solution unique sur [3/2;2].

Par la suite, il est possible de resserrer cet intervalle en calculant par exemple f(7/4),  7/4 étant le milieu de l’intervalle [3/2;2]. La calculatrice nous dit que f(7/4) ≃ -0,058 < 0 donc la solution, que l’on note souvent α, est telle que 7/4 < α < 2. En répétant cette méthode, appelée dichotomie, autant de fois que nécessaire, il est possible d’approcher α avec la précision souhaitée. En pratique on programme l’algorithme de la dichotomie, assez fastidieuse à faire à la main, sur une calculatrice ou un ordinateur ce qui donne un résultat avec plusieurs chiffres après la virgule en une fraction de seconde. Il existe d’autres méthodes plus élaborées qui convergent plus rapidement (c’est-à-dire qui ont besoin de moins de calculs pour la même précision) comme la méthode de la tangente de Newton. Celle-ci pourra faire l’objet d’un prochain billet !